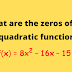There are different methods of finding the zeros of a quadratic function.
We learn about them with some examples:
What are the zeros of the quadratic function f(x) = 8x^2 – 16x – 15?
The given quadratic function is $ f(x) = 8x^{2} - 16x - 15 $
We have to find the zeros of this function.
For this purpose, we will use the Quadratic Formula.
We know that the standard form of a quadratic function is $ ax^{2} + bx + c $ .......(1)
where a, b, c are constants.
The Quadratic formula is $ x = \frac{- b \pm \sqrt{b^{2} - 4ac}}{2a} $ .......(2)
where the sign $ \pm $ shows that a Quadratic function has two zeros.
Comparing the given Quadratic function with (1) we get,
$ a = 8, b = -16, c = -15 $
Now putting the values of a, b, c in (2) we get,
$ x = \frac{- b \pm \sqrt{b^{2} - 4ac}}{2a} $
or, $ x = \frac{- (-16) \pm \sqrt{(-16)^{2} - 4(8)(-15)}}{2(8)} $
or, $ x = \frac{ 16 \pm \sqrt{256 + 480}}{16} $
or, $ x = \frac{ 16 \pm \sqrt{736}}{16} $
or, $ x = \frac{ 16 \pm 4\sqrt{46}}{16} $
or, $ x = \frac{ 4 \pm \sqrt{46}}{4} $
or, $ x = \frac{ 4 + \sqrt{46}}{4},\frac{ 4 - \sqrt{46}}{4} $
Therefore the zeros of the quadratic function $ f(x) = 8x^{2} - 16x - 15 $ are $ x = \frac{ 4 + \sqrt{46}}{4},\frac{ 4 - \sqrt{46}}{4} $.
Also read: What are the zeroes of the quadratic polynomial 3x^2-48?
Which is a zero of the quadratic function f(x) = 16x^2 + 32x − 9?
To find the zeros of the quadratic function we the Factor method.
Writing the quadratic function as a quadratic equation and factoring we get,
$ 16x^2 + 32x − 9 = 0 $
or, $ 16x^2 + (36 - 4)x − 9 = 0 $
or, $ 16x^2 + 36x - 4x − 9 = 0 $
or, $ 4x (4x + 9) -1 (4x + 9) = 0 $
or. $ (4x + 9)(4x -1) = 0 $
or, Either $ 4x + 9 = 0$ or $4x - 1 = 0 $
Either $ 4x = - 9 $ or $ 4x = 1 $
Either $ x = \frac{-9}{4} $ or $ x = \frac{1}{4} $
Therefore the zeros of the quadratic function f(x) = 16x^2 + 32x − 9 are $ x = \frac{-9}{4} , \frac{1}{4} $
Also read: Find quadratic polynomial whose sum of roots is 0 and the product of roots is 1
What are the zeros of the quadratic function f(x) = 6x^2 + 12x – 7?
Given that $f(x) = 6x^{2} + 12x – 7$
We use the quadratic formula to find the zeros of a quadratic function.
Comparing the given quadratic function with $ax^{2}+bx+c=0$ we get
a = 6, b = 12 and c = -7
Now putting these values in (2) we have,
$x = \frac{- b \pm \sqrt{b^{2} - 4ac}}{2a}$
or, $x = \frac{- 12 \pm \sqrt{(12)^{2} - 4(6)(-7)}}{2(6)}$
or, $x = \frac{- 12 \pm \sqrt{144 + 168}}{12}$
or, $x = \frac{- 12 \pm \sqrt{312}}{12}$
or, $x = \frac{- 12 \pm 2 \sqrt{78}}{12}$
or, $x = \frac{- 6 \pm \sqrt{78}}{6}$
or, $x = \frac{- 6 + \sqrt{78}}{6}, \: \frac{- 6 - \sqrt{78}}{6}$
Therefore the zeros of the quadratic function $f(x) = 6x^{2} + 12x – 7$ are $x = \frac{- 6 + \sqrt{78}}{6}, \: \frac{- 6 - \sqrt{78}}{6}$